The U.S. Spent Nuclear Fuel Policy: Road to Nowhere [Part III: Yucca Mountain]

By Robert Peltier -- July 10, 2010

Part I explored the historical context of the U.S. nuclear waste storage policy, while Part II reviewed the 1960s Salt Vault project.

This post looks at the legislative history of the ill-fated Yucca Mountain repository and the formation of a committee to explore alternative storage sites (again). In Part IV, we will look at some of the legal and political repercussions of Yucca Mountain’s failure.  Finally, in Part V, we explore failed attempts to reprocess nuclear fuel in the U.S. and examine the global state-of-the-art reprocessing plants now operating or under construction.

The Retrievable Surface Storage Facility

The AEC announced plans (circa May/June 1972) to construct an engineered, at-grade Retrievable Surface Storage Facility (RSSF) to be used until a permanent geological repository would be available. The plan was to locate the RSSF at an AEC or federal site in the western U.S. However, the environmental impact statement (EIS) issued by the AEC in support of the RSSF concept drew intense criticism from the public and the Environmental Protection Agency (EPA). Both criticized the plan because of the possibility that economic factors could later dictate using the facility as a permanent repository, contrary to the planned interim use of the RSSF. In this instance, it was unacceptable to proceed with an interim storage system unless there were unambiguous assurances that a permanent repository would be developed.

In 1975, Dr. Robert Seamans—in one of his first acts as administrator of the Energy Research and Development Administration (ERDA)—withdrew the EIS associated with the RSSF and decided that a permanent waste repository should be given budget priority. ERDA was created to assume the responsibilities of the then-dissolved AEC that were not covered by the newly formed NRC.

In 1976 a multiple-site strategy was initiated that would have led to the development of several repositories by 2000. Letters were sent to 36 state governors, informing them of these plans and asking for their cooperation in site exploration activities. A number of generic studies were undertaken at the Nevada Test Site, the Permian Basin and Palo Duro sub-basin in Texas, and Salina Basin in Michigan, Ohio, and New York. Exploration of specific sites would begin in Texas, Louisiana, Mississippi, Washington, and Nevada for the site that would host the first commercial waste repository.

As a group, these states realized the importance of becoming more intimately involved in the nuclear waste management decision-making process. ERDA offered to work closely with the states and to keep the governors informed of how its programs were progressing. It also promised to terminate a project within a state if technical issues were not resolved through mutually accepted procedures. The states, in effect, were being offered what they believed to be veto power over construction of a waste facility within their jurisdiction. Thus, what began as a new initiative to involve states in participative decision-making soon devolved into individual states halting projects because they were reluctant to consider a facility in their state.

The AFR Storage Concept

Because of the geologic disposal program’s relatively late start and the federal government’s deferral of commercial reprocessing, concerns were raised that a number of operating reactors would run out of room to store their spent nuclear fuel (SNF) on-site. Should that occur, and if there were no alternative locations for storing the SNF, the reactor would be forced to shut down. To address this particular concern, and while ERDA was reorganized into the current DOE, in 1977, ERDA pursued an “away-from-reactor (AFR) storage” concept for any spent fuel that utilities wished to transfer to the federal government. The government would then take title to the fuel and be responsible for its permanent disposal. At the time of transfer, the utilities would pay a one-time charge that would fully pay for storage and disposal costs.

The AFR concept was initially designed to serve four different functions: preventing the shutdown of reactors pending repository development; providing time for the geologic disposal program to mature; allowing the U.S. to accept limited amounts of foreign spent fuel to achieve nonproliferation objectives; and maintaining access to plutonium and uranium in the SNF should reprocessing become viable again in the future. However, the AFR concept was viewed very much as the RSSF concept had been several years earlier. The result was also similar: The project was terminated in 1981.

Nuclear Waste Policy Act

In 1982, Congress enacted the Nuclear Waste Policy Act, which was signed by President Ronald Reagan on January 7, 1983. The NWPA represented the most expensive civil works project in history, establishing a schedule for the DOE to site and for the NRC to license geological repositories for permanent disposal of SNF and high level nuclear waste (HLW). The DOE was directed to assess numerous locations around the country for possible sites and present a minimum of three finalist sites. Although this legislation was a decisive step forward, its attempted implementation again raised a public outcry based on accusations that government agencies were acting in secret to identify storage sites.

To finance the project, the NWPA established the NWF, to which electricity consumers would pay a fee of one-tenth of a cent for every nuclear-generated kilowatt-hour of electricity consumed. The DOE would draw upon the NWF to finance the siting, construction, and operation of repositories. In exchange for payment into the NWF, the DOE was required to take title to the SNF and HLW following the opening of the first repository — scheduled for January 31, 1998.

In February 1983, the DOE carried out the first requirement of the NWPA by formally identifying nine potentially acceptable locations (the host rock is shown in parentheses), for the first repository:

· Vacherie dome, Louisiana (domal salt)

· Cypress Creek dome, Mississippi (domal salt)

· Richton dome, Mississippi (domal salt)

· Yucca Mountain, Nevada (welded tuff)

· Deaf Smith County, Texas (bedded salt)

· Swisher County, Texas (bedded salt)

· Davis Canyon, Utah (bedded salt)

· Lavender Canyon, Utah (bedded salt)

· Hanford Site, Washington (basalt flows)

By 1984, the DOE believed that one or more repositories would be available by 2007 – 2009 and that sufficient repository capacity would be available 30 years beyond the expiration of any reactor operating license to dispose of SNF and HLW generated during that time. In addition, the DOE reaffirmed its obligation to accept SNF assemblies beginning in January 1998, whether or not a permanent disposal facility was ready. This announcement was to enable utilities to plan for their projected waste disposal needs with confidence and certainty.

After evaluating the nine candidate sites, the DOE selected three finalists: Yucca Mountain, Deaf Smith County, and Hanford. These sites advanced into the next round of intensive scientific study described as the “site characterization process.” Critics had claimed the sites were recycled from surveys performed in the 1970s and that the NWPA required the DOE to conduct a new screening process rather than proceed with sites considered prior to the passage of the NWPA. On May 28, 1986, President Ronald Reagan approved Yucca Mountain for site characterization under the NWPA. By that time, nearly $1.5 billion had been spent surveying, drilling, recording seismic information, monitoring, and analyzing the Yucca Mountain site.

Nuclear Waste Policy Amendments Act

President George H.W. Bush signed the NWPAA on December 22, 1987, which supposedly “settled” the waste storage issue by codifying the Yucca Mountain site in Nevada as the nation’s first geological waste nuclear fuel repository. Characterization of each site had been estimated to take five to seven years, costing somewhere around $1 billion to $2 billion, so work on the other two finalist sites was postponed indefinitely.

The NWPAA outlined a detailed approach for disposal involving review by the president, Congress, state and tribal governments, the NRC, and other federal agencies, while retaining the 70,000 metric ton limit on the amount of SNF and HLW that the DOE could place in the first repository. According to the amendment’s legislative history, the intent of this limitation was to ensure that no state would have to bear the entire nuclear waste disposal burden. The DOE also extended the timetable for opening the first repository from 1998 to 2003. However, if Yucca Mountain was found to be unsuitable, Congress was to be notified and provided alternatives.

Regional Equity Concerns

Regional equity concerns were raised because a majority of the SNF was being generated in the eastern U.S. while all of the final repository candidate sites were located in the west. At one time, however, there were 12 potential sites for a second repository in seven eastern states.

To counter the regional equity issue, a monitored retrievable storage (MRS) facility would be integrated into the ultimate disposal system and preferably be located in the eastern U.S. Also, the licensing process would be straightforward because the MRS did not have to isolate wastes for thousands of years but simply serve as a temporary, multi-decade storage facility; then shipments would be consolidated in dedicated trains and trucks taking waste to the repository.

Three sites had been identified in Tennessee, with the preferred site being Oak Ridge, which was originally identified for the postponed Clinch River breeder reactor in 1983 when funding was terminated. The State of Tennessee was against designating Tennessee alone as a contender and sued. The proposal was held up and ultimately went to the Supreme Court. The DOE won the case and submitted its proposal to Congress.

Nevertheless, in order to prevent the MRS from becoming a de facto repository — similar to the RSSF and AFR facility — the DOE recommended certain conditions linking MRS development to repository development. The license for the MRS would contain conditions allowing construction and operation of the MRS only when repository construction and operation was proceeding and would limit the total capacity of the MRS to 15,000 metric tons of waste.

The NWPAA had also established the Office of the Nuclear Waste Negotiator to negotiate agreements with states or Indian tribes willing to host a repository or an MRS. Such an agreement could contain different conditions than those imposed on a DOE-sited facility. However, the office was not reauthorized by Congress and was eliminated in 1995.

The Yucca Mountain Saga

Between 1987 and 2001, the DOE would spend another $3.8 billion on scientific and technical studies of Yucca Mountain. For instance, in 1997, a 5-mile tunnel through Yucca Mountain was completed to function as an Exploratory Study Facility. In 1998, a second 2-mile cross drift tunnel would facilitate additional experiments in the potential repository host rock. These tunnels, and the numerous niches and alcoves, created the world’s largest underground laboratory (Figures 1 and 2).

1. View of the South Portal of the Exploratory Studies Facility showing the 25-foot-diameter tunnel boring machine. Source: DOE/OCRWM

2. Tunnel boring machine cutter head at the South Portal in April 1997. Source: DOE/OCRWM

From the surface, more than 180 boreholes were drilled deep into the geology and its surrounding features. Independent scientists working for Nye County, Nevada, drilled additional exploratory holes and collaborated with DOE scientists on their findings. These efforts were further supplemented by numerous laboratory experiments and excavation of similar geologic features both nearby and at sites around the world. The results ultimately provided an understanding of the Yucca Mountain geology and its ability to safely contain radioactive wastes.

In 2001, the DOE issued reports containing thousands of pages of information, summarizing the extensive site characterization effort. Over the next year, the department would hold more than 65 public hearings, sending 6,000 letters to individuals, corporations, and groups, eventually responding to more than 17,000 comments. In 2002, President George W. Bush approved the secretary of energy’s recommendation of Yucca Mountain as the site for a nuclear fuel repository.

In April 2002, Governor Kenny Guinn (R) of the State of Nevada, as provided for by the NWPA, vetoed this decision. In the NWPA’s unprecedented procedure for ensuring that any site decision received thorough and fair consideration, the governor’s veto could only be overridden by a majority vote in both houses of Congress. For three months, Yucca Mountain was debated in Congress, in committee hearings, and on the floor of the House and Senate. Eventually, Congress would vote to override the objection by approving the Yucca Mountain site 306-117. Later, the Senate would approve the Yucca Mountain site by voice vote following a procedural “motion to proceed” vote, 60-39. This approval, known as the Yucca Mountain Development Act (YMDA), was signed into law by the president on July 23, 2002, allowing the DOE to prepare and submit a license application to the NRC.

By the time the YMDA was enacted, the DOE had spent $7.1 billion on the evaluation of multiple sites, detailed study of Yucca Mountain, the preparation and defense of the site recommendation, and related waste acceptance and transportation planning activities. It would spend another $1.5 billion preparing the Yucca Mountain license application, including transportation and waste acceptance plans. After years of delay, the DOE submitted the 8,600-page license application to the NRC in June 2008 (Figure 3).

3.    The Yucca Mountain license application. Source: DOE/OCRWM

After a preliminary 90-day screening period, the NRC determined that the application contained sufficient information to formally docket the application and move on to the next stage of technical and scientific review. Approximately 40 NRC staff members and consultants reviewed the license application prior to the docketing decision. The license application was not reviewed for merit during this screening period, but rather to determine whether it was complete enough for the NRC to proceed.

According to federal legislation, the NRC must complete the Yucca Mountain license application review within four years. However, there is no penalty if the NRC fails to finish the review within the required time period. According to the DOE, the earliest the repository could start accepting waste, given a smooth licensing process and consistent funding, was 2020. The total system life-cycle cost that includes the cost to research, construct, and operate Yucca Mountain for 150 years, from the beginning of the program in 1983 through closure and decommissioning in 2133, was estimated to exceed $96 billion.

The Only Option Remaining: On-Site Storage

Today, the only available solution for utilities is to store SNF on-site in water pools or in long-term above-ground storage casks. The volume of the water pools within each reactor limits the number of fuel assemblies it can hold at one time. Conceptually, the number of dry casks that can be used to store SNF is unlimited.

The water-pool storage option involves storing SNF assemblies under at least 20 feet of water to provide shielding from the radiation and removal of decay heat (Figure 4). About one-fourth to one-third of the total fuel load is removed from the reactor, typically every 18 months, and replaced with fresh SNF. You may recall that early in the development of commercial nuclear reactors, the government was expecting to construct a nuclear fuel reprocessing plant and the pools were sized to hold and cool SNF until it could be transported to the reprocessing facility. On April 7, 1977, President Jimmy Carter banned the reprocessing of commercial reactor fuel in the U.S. Since then, many of the nuclear plant spent fuel pools have either reached or are nearing capacity (Figure 5).

4. Storing spent fuel assemblies underwater in a storage pool. Source: DOE

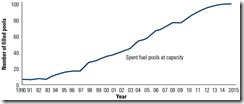
5. This chart shows the cumulative number of filled pools at nuclear power plants. All operating nuclear power reactors are storing used fuel under NRC licenses in spent fuel pools. Some operating reactors are using dry cask storage. Source: NRC

Current regulations permit re-racking of the storage pool grid and fuel rod consolidation, subject to NRC review and approval, to increase the amount of SNF that can be stored in a pool. However, both of these methods are constrained by the size of the pool.

In the early 1980s, utilities began looking at using dry casks to increase on-site storage capacity. The process of loading a cask, consisting of a steel cylinder designed to hold typically two dozen SNF assemblies, takes place underwater in the storage pool. Once the assemblies have cooled for given period of time, they are transferred underwater from the storage racks to the submerged cask. Next, the cask is removed from the storage pool, where excess water is removed. Then it is backfilled with an inert gas to enhance decay-heat transfer capabilities, welded or bolted closed, inserted into a concrete overstructure (depending on design), and stored vertically on a concrete pad. The cask itself provides the necessary radiation shielding. Other above-ground designs seal the SNF inside a steel cylinder, which is then inserted either vertically into a concrete silo or horizontally into a concrete vault. The concrete provides the radiation shielding (Figure 6).

6. Spent nuclear fuel storage canisters are designed to be placed either vertically in aboveground concrete or steel structures, or stored horizontally in aboveground concrete vaults. Courtesy: NRC

The NRC approves dry-storage systems by evaluating each design for resistance to accident conditions such as floods, earthquakes, tornado missiles, and temperature extremes. Some cask designs can be used for both storage and transportation. The dry-storage casks are located in an independent spent fuel storage installation (ISFSI). Such storage may be either at the reactor site or elsewhere.

Site-Specific and General Licenses

The NRC authorizes storage of SNF at an ISFSI under two licensing options: site-specific licensing and general licensing. Under a site-specific license, an applicant submits a license application to the NRC, and a technical review is performed on the safety aspects of the proposed ISFSI. If the application is approved, the NRC issues a license that is valid for 20 years. The license contains technical requirements and operating conditions (including fuel specifications, cask leak testing, surveillance, and other requirements) for the ISFSI and specifies what the licensee is authorized to store at the site.

A general license authorizes a nuclear plant licensee to store SNF in NRC-approved casks at a site that is licensed to operate a power reactor under 10 CFR Part 50. Licensees are required to demonstrate that their site is adequate for storing SNF in dry casks. The licensee must also make any necessary changes to its security program, emergency plan, quality assurance program, training program, and radiation protection program to incorporate the ISFSI at its location. In addition, these evaluations must show that the cask’s technical specifications covered in the Certificate of Compliance (CoC) can be met, including analysis of earthquake intensity and tornado missiles (objects accelerated by very high winds). The NRC issues a CoC to the vendor following a technical review and approval of a dry storage system’s design in accordance with 10 CFR 72. The certificate expires 20 years from the date of issuance and can be renewed in additional 20-year increments.

The first U.S. commercial ISFSI was licensed by the NRC in 1986 at the Surry Nuclear Plant in Virginia. Since then, dry cask storage has become common among licensees needing additional SNF storage capacity. According to the NRC, SNF is currently in dry storage at 40 general license ISFSIs and 15 site-specific license ISFSIs. For example, Southern Nuclear’s Hatch and Farley nuclear plants safely store spent fuel in above-ground dry storage casks (Figure 7).

7. Southern Nuclear’s dry-cask storage system at Hatch Nuclear Plant. Courtesy: Southern Nuclear

Southern Nuclear is the operator of the Vogtle nuclear plant. At Vogtle, all of the used fuel for both units is stored safely under water in two storage pools located in the protected area of the plant. There is still storage capacity available in the existing pools to last for years. Therefore, by combing the existing capability of the storage pools and dry-storage facilities when the spent fuel pool does reach capacity, all of Southern Nuclear’s sites have the capability to safely store spent fuel on-site for the duration of each plant’s operating license.

Part IV will review the legal and political impact of the Yucca Mountain failure.

Portions of this post were first published in POWER magazine and co-authored with Contributing Editor James Hylko.